A DIALOGUE ON WHAT MAKES FE AN FE

Student: You said all numerical techniques are based on the same philosophy that is to convert the continuous nature of the DE into algebraic simultaneous equation. So what makes FE an FE, in other words, what differentiates FE from the rest of the numerical techniques?

Dr Airil: What makes FE and FE, in other words, what differentiates FE from the rest of the numerical techniques is the use of predefined shape functions.

Student: That's it?

Dr Airil: Yes, that is about it.

Student: What about the use of degree of freedom or dof?

Dr Airil: The use of dof in FE is a standard math terms actually, it is equivalent to nodal values as in Finite Difference and other techniques. In fact the words dof and nodal values are themselves interchangeable.

Student: What about Galerkin (or weighted residual method, WRM) formulation, is not it characterizes FE?

Dr Airil: Yes but not uniquely, many other numerical techniques employ Galerkin (or WRM for that matter) like Boundary Element Method or BEM and Meshfree (or Meshless) method. In fact, FEM itself can be derived from various sources like principle of virtual works and minimum potential energy.

Student: So, it is the use of predefined shape functions that differentiates FE from the rest of the numerical techniques. This what makes FE an FE.

Dr Airil: Yup.

Student: Thanks

Dr Airil: You are welcome.

A DIALOGUE ON NUMERICAL TECHNIQUES

Student: What is numerical technique?
Dr Airil: Numerical technique is a method for solving DE in an approximate but converging manner.

Student: What do you mean by approximate and converging?
Dr Airil: Approximate as opposed to analytical whilst converging means the increase in the degree of accuracy due to the increase in the number of terms or orders of the 'trial' function.

Student: What is a 'trial' function.
Dr Airil: A 'trial' function is a function that we 'guessed' to be the solution of the DE.

Student: Why we must 'guess' a function for a solution of the DE?
Dr Airil: We must guess because if we know the solution already, then we would not have the problem in the first place, would we?

Student: How numerical technique works, in other words, what is the basic idea of numerical technique?
Dr Airil: The basic idea of any numerical techniques is to convert the continuous nature of the DE into a set of algebraic simultaneous equations, then usually treated and solved by matrix operation.

Student: How this conversion is done?
Dr Airil: This is done by first, assuming for a 'trial' function which consists of coefficient/constant and the independent variables i.e. x, y, z. For example, a1+a2x+a3x^2 is a form of 'trial' function usually used. Secondly, insert this 'trial' function into the DE by conducting the appropriate differentiation. Such an insertion will turn the DE from its differential forms into ordinary function. Let's call this function as R. Thirdly, evaluate this function, R by either integrating it or by collocating it and set it to zero. The latter refers to evaluating R at certain locations say L1, L2. These evaluation process will convert the independent variables i.e. x,y,z into numerical values, leaving the coefficient/constant i.e. a1, a2, b1,b2 etc as the unknown variables which differ from previous x,y,z in the sense that these variables are constant in nature. Due to this constant property, the final product of the whole process is algebraic thus allows for its treatment in matrix forms. This is the basic idea of any numerical techniques.

Student: What are the examples of numerical techniques?
Dr Airil: As I have told you before, examples of numerical techniques are the Finite Difference, Boundary Elements and of course Finite Element. And recently, a new family of techniques has emerged called Meshfree techniques. But, as far as I have experienced it, among these techniques, Finite Element is the most robust and versatile and will survive the test of time.

Student: You keep mentioning about the matrix treatments, why?
Dr Airil: I keep mentioning about the matrix treatment because this is the essence of numerical technique. The matrix treatments or operations are beneficial in the following ways, 1) suits computer programming, 2) allows compact mathematical representation of a complex problem.

Student: Can you elaborate on the two points?
Dr Airil: On point 1), you see, matrix operation and computer programming complement each other. Whilst the knowledge of matrix has been known as early as the beginning of 1900's but its practical applications were 'retarded' I would say due to the ongoing development of the computer technology. The later establishment of computer would then 'burst' the application of matrix operation. But in turn, the development of the computer itself was very much influenced or 'guided' by the potential borne by the knowledge of matrix. If I am not mistaken, Heisenberg once said something like, matrix is the most beautiful mathematical tool and this was before the start of any works on computer development. The father of computer, John Von Neumann was a mathematician heavily influenced by matrix. So matrix and computer is like chicken and egg, you know what I mean.
On point 2), although the basic principle is not difficult, but the use of numerical technique will lead us to deal with huge and complex physical problems. But, with the availability of matrix representation, the 'length' of the equations can still be made as if it is still 'short' hence the terms compact. As a result of such a compactness, we can still 'do the calculation in our head' regardless of how big and complex the physical problem would be.

Student: Thanks.
Dr Airil: My pleasure.

MY OWN SONG (SYUKURKU)

Lagu untuk Lynn. Aku syukur sangat pada Allah sebab izinkan dia jadi isteri aku,

MY OWN SONG (CERIA DI UTM)

Lagu untuk semua ex-utm dan students utm

MY OWN SONG (RINDU PADA MU)

Lagu ni aku buat waktu Lynn dan anak2 balik Malaysia kali kedua. Aku rindu sangat.

MY OWN SONG (KASIH MU)

Lagu untuk Lynn. Her love is my strength.

MY OWN SONG (RUANG)

Aku buat lagu ni waktu Lynn dan anak2 balik Malaysia kali kedua. Aku macam nak gila balik rumah, sunyi sangat!!!

RUANG ( written by Dr Airil Sametok)

 Verse 1:

Aku di ruang kosong 

Dikeliling dinding sepi

Sekosong hati ini

Ruang yang dulu penuh 

Dengan hiasan hidupku

Kini tidak berwarna

Chorus:

Tiada lagi hati-hati yang rindu

Tiada lagi jiwa-jiwa menunggu

Yang tinggal hanya gema-gema suara

Yang memanggilku hampir padanya

Verse 2:

Hanya tinggal kenangan 

Saat-saat manis kita

Di ruang ini pernah bersama

Hanya tinggal bayangan 

Senyum-senyum yang terakhir

Mencengkam hati ini

                                                                        Ulang chorus....

MY OWN SONG (SELAMAT TINGGAL UTM)

Aku itu hari nak blah sangat tapi tak jadi. It was not time yet.

MY OWN SONG (MAK DAN AYAH)

Lagu ni aku buat untuk mak ngan ayah dan adik2 waktu kat UK. Rindu sangattt!!! (Lyrics below)



Kau jauh terlalu jauh dariku
Sendiri memendam rindu padamu
Di bumi asing, ku coret puisi rindu
Menjadi selimut kedinginan ku

Kau jauh, jauh mu beribu batu
Lautan yang memisah kau dan aku
Hanya ku pasrah pada takdir yang menentu
Waktunya ku kembali kepada mu

chorus:

Oh kasih, usahlah berduka
Ini hanya sementara,
Walau kau jauh di mata
Kenangan bersama tersemat di dada

Oh kasih, usahlah kau resah
Terus sajalah berdoa
Jangan kau resah menunggu
Bila sampai waktu kembali bertemu

Ku tempuh hari hari yang berlalu
Di bumi asing ku korban hanya untuk mu
Demi mencapai impian dan cita cita
Untuk ku hadiah pada ibunda

MY OWN SONG (JAUH BEGINI)

Lagu ni aku buat waktu Lynn dan anak2 balik Malaysia kali pertama. Rindu sangatt!!!

MY 2011 PUBLICATIONS

Its the time of the year again when everybody is busy reporting to their bosses this year performance or KPI. I am no different. Today I have submitted my list of publications to my centre, STC as requested (although I am a week due). Not much really because I have been consumed by ERCAD development but Alhamdullillah, at least there are still something for me to report as far as publications are concerned. The list is given below for your viewing (since it is in ready 'cut-and-paste' forms, why do not I put it as an entry, right?) and I have divided them into two fields; structural mechanics and fluid dynamics.


STRUCTURAL MECHANICS

Journals

1. Muhammad N.H. Mahat, Ahmad.B.H Kueh, Nurhidayah Rasin, Airil Y. M. Yassin, and Hisham Mohamad (2011), Size Dependent Uniaxially Loaded Stability of Triaxial Weave Fabric, Composites,Applied Mechanics and Materials Vols. 94-96, pp 1742-1745.

Conferences

2. Muhammad N.H. Mahat, Ahmad B.H Kueh, Nurhidayah Rasin, Airil Y. M. Yassin, and Hisham Mohamad (2011), Size Affected Monoaxially Loaded Buckling of Triaxial Weave Fabric Composites, National Seminar on Civil Engineering Research.

3. Nurhidayah Rasin, Ahmad B.H Kueh, Muhammad N.H. Mahat, Airil Y. M. Yassin, and Hisham Mohamad (2011), Size Dependent Biaxially Loaded Stability of Triaxial Weave Fabric Composites, National Seminar on Civil Engineering Research.

FLUID DYNAMICS

Journals

4. Nursalasawati Rusli, Erwan H Kasiman, Ahmad.B.H Kueh, Airil Y. M. Yassin and Norsarahaida Amin, (2011), Numerical Solution of a Two-Dimensional Navier Stokes Equations using an Improved Finite Difference Method, MATEMATIKA, Vol 27, No. 1, 1-9

Conferences

5. Nursalasawati Rusli, Ahmad.B.H Kueh, Erwan H Kasiman, Airil Y. M. Yassin and Norsarahaida Amin, (2011), Numerical Computation of a Two-Dimensional Biomagnetic Channel Flow, International Conference on Mathematical and Computational Biology

P/S: If you wonder about Part 4 of HOW LEARNING CAN BE FUN, I am really working hard on it. It will be ready any time soon. InsyaAllah.

A DIALOGUE ON DIFFERENTIAL EQUATIONS

I am still actually working on the final part (Part 4) of HOW LEARNING CAN BE FUN. I am trying to end up the topic with an impact but frankly speaking, it is not easy. To finish what we have started is the most difficult part, isn't?

So to keep feeding this blog with material, I have decided to make this entry which is actually something that I have posted in an FB group called Dr Airil's Finite Element Forum. This forum was set up initially by a group of students who currently attending my class on FE. Now, this FB forum is opened for public. So herein, I like to invite the readers of this blog to join the forum by visiting http://www.facebook.com/groups/244071082308340/Basically, in this forum, the students, members and visitors are free to ask me any questions about Finite Element Method and I will try to answer them the best I can. Please visit and become a member. Lets hope that this forum can be an alternative and interesting way for us to know more about FEM.

So as an ice breaking for the forum, I have made a dialogue between me and an imaginary student who asks about differential equation. I share herein the dialogue for your reading. Please enjoy.

Student: What is a differential equation?
Dr Airil: Differential equation or DE is a mathematical statement that contains the relevant information about the physical problem at hand.

Student: Since it is contained, how can we get this information?
Dr Airil: We can get the information by solving the DE.

Student: How do we know that this information is correct?
Dr Airil: The information is correct if the DE is correct and if we solve the DE correctly.

Student: When a DE is correct and when it is wrong?
Dr Airil: A DE is correct if it is derived by satisfying the conservation laws of mass, energy and momentum. It is wrong when the derivation violates these laws.

Student: How can we solve a differential equation?
Dr Airil: We can solve DE in many ways but not all will work. We can solve analytically by direct integration, undetermined coefficient method etc. or semi analytically by Laplace Transform, Fourier Transform etc. or numerically by finite difference method, boundary element method and of course finite element method.

Student: Let's say that we have derived a new DE? How can we know whether it is right or wrong?
Dr Airil: Ok, let's say that we have derived a new DE, we then must solve it. The solution or the information that we just obtained by solving the DE remains as a hypothesis until we verify it. If verified, then we know that our DE is correct and we can claim to have our own new theory. Huh, how cool is that?

Student: But, how can we verify the solution?
Dr Airil: Basically, there are two major ways of verification of DE and its solution. One is by verifying it with experimental tests or physically measured data and two, by verifying it with an established solution of another DE which we can argue to certain extent the equivalency and representativeness between the two.

Student: Why DE is difficult to learn?
Dr Airil: It seems to be difficult because one, you are not told of the importance of DE and two, you are not told of the 'story' of DE. If you know these two (I hope by now you know at least a bit from our discussion), you will see how DE is actually very easy.

Student: You said that learning of DE can be easy if we know the importance. What is the importance of DE?
Dr Airil: As I said, DE contains information. These information if exploited can make all the changes in the world. You can build the fastest car, you can send people beyond mars, you can make new medicine, and you can do all the good things. Actually, understanding and exploiting DE are what differentiate us from the advanced countries. Wallahualam.

Student: Thanks
Dr Airil: Don't mention it, my pleasure

MY PUBLICATIONS WITH PROF NORSARAHAIDA

Herein is the list of my papers which I wrote together with Professor Norsarahaida Amin and our colleagues . She was the Head of Mathematics Department before being promoted to her current post the Deputy Dean of the Faculty of Science, UTM. I have been working with her about three years now and I am so honored to have her as my mathematics mentor.

I should also introduce the other authors. Dr Ahmad K B Hong and I, are in the same department at FKA. He obtained his PhD from Cambridge under the supervision of Prof Pellegrino who is now a professor in CALTECH. Dr Ahmad an I have written nine papers together and two lectures note on FE and Computational Mechanics. He is a year younger than me.

Nursalawati and Rosliza are PhD students registered at Mathematics Department of UTM. Nursalawati is a UNIMAP lecturer whilst Rosliza teaches in UiTM. Nursalawati works on improving Finite Difference Approach in modelling the effect of stenosis to blood flow whilst Rosliza is formulating Finite Element approach to tackle the problem of fluid-structure interactions between the blood flow and the blood vessel in the study of aneurysm.

Erwan Kasiman has submitted his Master's thesis which involved the derivation of Finite Element Formulation in allowing for the inclusion of magnetic fields in the Navier-Stoke flow's equation. He is now a tutor of FKA.

The papers below basically involve mathematical formulations and the writing of subsequent computer source's code. The occasional use of existing engineering software are merely for verification purposes; to verify the derived formulations and written source's code.

Journals

1. Nursalasawati Rusli, Erwan H Kasiman, Ahmad K B Hong, Airil Y M Yassin and Norsarahaida Amin, (2011), Numerical Solution of a Two-Dimensional Navier Stokes Equations using an Improved Finite Difference Method, MATEMATIKA, Vol 27, No. 1, 1-9

Keynote

1. Airil Y M Yassin, and Norsarahaida Amin, (2009), The Importance of Engineering Mathematics, Engineering Mathematics Seminar, UKM

Conferences

1. Nursalasawati Rusli, Ahmad K B Hong, Erwan H Kasiman, Airil Y M Yassin and Norsarahaida Amin, (2011), Numerical Computation of a Two-Dimensional Biomagnetic Channel Flow, International Conference on Mathematical and Computational Biology

2. Nursalasawati Rusli, Sasa Kenjeres, Airil Y M Yassin, Ahmad K B Hong and Norsarahaida Amin, (2010), Three Dimensional Numerical Simulations of Blood Flow Behaviour in Stenotic and Aneurysmal Arteries, 1^st Regional Conference on Applied and Engineering Mathematics, UNIMAP

3. Nursalasawati Rusli, Erwan H Kasiman, Airil Y M Yassin, Ahmad K B Hong and Norsarahaida Amin, (2010), Numerical Computation of a Laminar Flow in a Straight Rectangular Duct, Faculty of Science Postgraduates Conference, Ibnu Sina Institute, UTM

4. Rosliza M Yasin, Erwan H Kasiman, Airil Y M Yassin, Ahmad K B Hong and Norsarahaida Amin, (2009), Ferrohydrodynamics Effects on One-Dimensional Acoustic Fluid Flow with Fluid-Structures Interaction, ICORAFSS

MY 'ONENESS' PARADOX IS WRONG

(this writing is a continuation of a previous entry, click I BELIEVE I HAVE EXTENDED HILBERT' PARADOX)

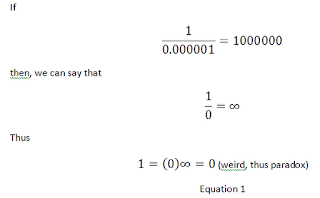
Damn, my paradox is wrong.

Yesterday, I went to see Dr Zainal (Head of Math. Dept) and Prof. Norsarahaida (Deputy Dean, Fac. of Science) to discuss about my ‘Oneness’ paradox. We met in Prof Sarah’s office and in no time they showed me where I got it wrong. By the way, Prof Sarah was quite upset because I only mentioned Dr Zainal in my previous post but not her (of course she was joking). For your information, Prof. Sarah and I have written six papers together and I am co-supervising two of her PhD students. Herein, I would like to express my gratitude to Prof. Sarah for being my mentor and it is my greatest honor to work with her for the past three years. I have posted the list of our papers in this blog for your viewing, just click here.

So, where I got it wrong? It was as early as Equation 1, as shown below.

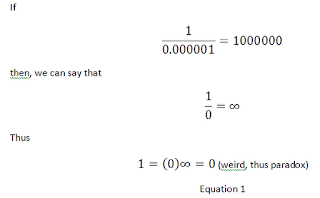
Why is it wrong? It is wrong because zero multiplied by infinity is not zero, but undefined instead. So since this equation is wrong, what follow are therefore wrong.

You see, infinity is not a number but instead, it is a concept or notion, created by us human so as to comprehend something that is never end. So, since infinity is not a number, you can not equate it to be equaled to anything except under the strict rule of limit expression as below:

Equation 2

This is therefore the collapse of my paradox. But having said this, the same argument also collapses Hilbert’s Paradox since he also argued by equating infinity to a number; only that I have overlooked such an argument before.

But, both Prof Sarah and Dr Zainal agreed that my attempt to imagine the two balls as tool for argument might help in the understanding of the concept of ‘undefined’ itself. What is it mean to be ‘undefined’? Another way to put it, what ‘defined’ means? As you going to see, we will be talking about ‘meaning’ itself.

By using the balls analogy, it is easier for technical men like me to imagine the whole process of the argument. Let me rewrite the Newton’s Inverse Law of Gravitation as follows:

Equation 3

What Equation 3 tells us is that, as the distance between the two balls got smaller, the force got bigger and bigger. These changes are all still comprehensible until the distance become zero at which the magnitude of F is conceptually prescribed as infinite. This is a typical explanation; there is nothing new about it. In fact, you might have heard it thousand times.

But, by imagining the two balls, we can have an alternative explanation. What we can say is, as long as there is a finite distance between the two balls, the concept of a ball remains valid, comprehensible thus defined. But when there is no more distance, a ball loses it concept. We can no longer define what happened to something which we used to call a ball. If we extend this discussion into higher dimensions, say into our familiar three dimensions, what we can say is that, a ball can be defined if there is a space for it (please take note that our previous discussion of a distance corresponds to a space in 3-dimensional region). If the space seizes to be finite, thus zero, although the ‘ball’ still exists (zero times infinity is not zero remember so the ‘ball’ does not diminish), it becomes ‘undefined’. We lose the ‘concept’ of meaning.

What we can deduce or learn from this are:

1. Our mathematics are handicapped thus valid only in a finite space (or space-time) which we currently live in, so do not ‘believe’ in mathematics, just use it

2. Since we possess the concept of meanings, then the universe must be finite (of course this is in agreement with present physics). This is because, if we have an infinite distance between the two ball, we will go back to Equation 1, where things are similarly undefined or become meaningless

3. There is existence ‘beyond’ the limit of infinity only that, this existence is not comprehensible through our mathematics. By now, we should have perceived the word ‘beyond’ the same way we perceive ‘infinity’; it should not be a ‘distance’ or anything like that, else we would have meaning out of it.

As conclusions, I hope that my writings somehow able to shed some light on some aspect of mathematics especially on the ‘lacking’ and ‘incompleteness’ of the mathematics itself. But, this does not mean that mathematics is evil or anything like that. How can a man like me say that? Instead, I promote everyone to learn mathematics to the deepest degree so that we can learn ‘how stupid we are’ actually as a human being. And as I said in point 1 we must use or exploit or manipulate mathematics to our advantages because somehow we still have to live in this world although temporarily. So while we are waiting for another life, exploitation of mathematics for the sake of goodness is what we have to do. As an analogy, a man who used to have a knee problem can now pleasantly ‘sujud’ and can be more ‘khusyuk’ in solat after a knee operation; a technology evolved due to the advert of ‘mathematics. You know what I mean?

Finally, I must say this, when I said ‘meaning’ I refer to those concepts comprehensible through the ‘exploitation’ of our five senses (aren’t our mathematics are built on these senses, are they?) and not the ‘TRUE MEANING’. For the ‘true meaning of existence beyond the realms of our mathematics’, we as a Muslim must therefore resort to the ultimate truth, sent to us through prophet Muhammad SAW, that is Al-Quran. Al-Quran is therefore THE ONLY AND THE ULTIMATE TRUTH, granted to us by ALLAH SWT so that we can know what we are allowed to know about the things that we can never know through our handicapped mathematics.

Wallahhualam.

REFINEMENT OF DISCUSSION (made on Saturday, 22 October)

Actually, my line of argument in the previous Oneness paradox is not all wrong. Yes, the final part of Equation 1 is wrong, that is

Equation 4

as it should be below

Equation 5

What this means is, whilst the previous Figure 2 is wrong (given again as below):

Figure 2

the following below is however correct:

Figure 3

So, although in the Oneness paradox we have wrongly argued (derived from Equation 4 and Figure 2):

“How two existences (referring to the two balls) can ever be described by a single existence?”

as far as our new discussion on meaning is concerned, the following statement is valid (as it is derived from Equation 5 and Figure 3):

“How two existences (referring to the two balls) can ever be described as undefined (or meaningless) ?”

hence the ground for our argument on ‘meaning’ as outlined in this entry. And, if we still want a paradox, let's call it 'MEANINGLESS PARADOX'. Huh, how about that?